一.标准化

1.标准化方程

最常用的标准化就是Z-Score标准化，简单理解就是减均值，并除以标准差。用方程表示如下：

其中，$\mu$是样本均值，$\sigma$是样本标准差。

2.标准化可视化

标准化的过程分为2个步骤，第1步是减均值，第2步是除以标准差。可视化分析如下：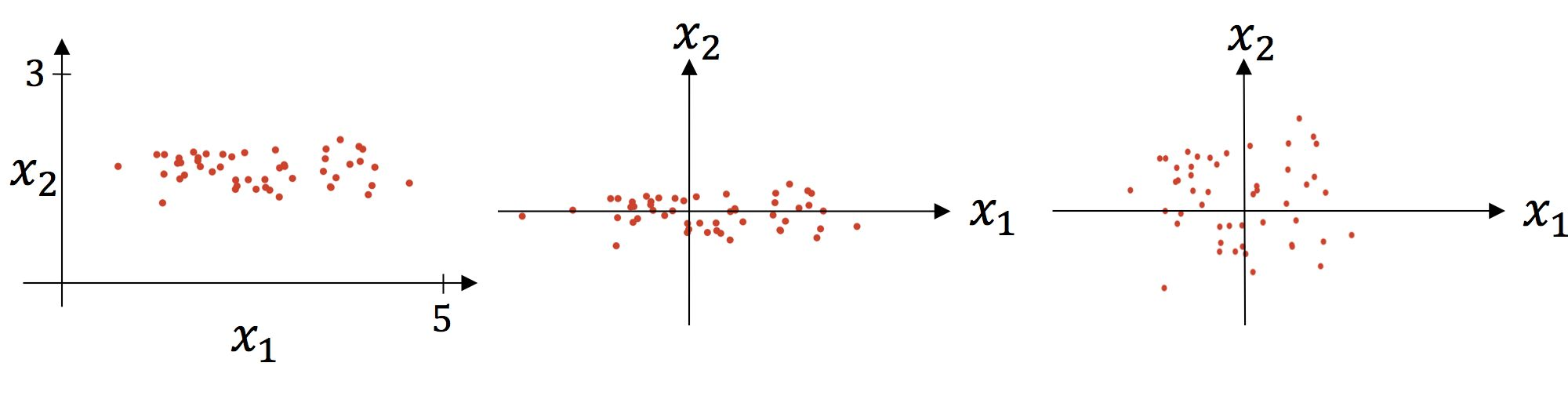

上图中左图是原图可视化，中图是减均值后的可视化，右图是除以标准差后的可视化。

3.标准化实现

from sklearn import preprocessing
import numpy as np

X_train = np.array([[1., -1., 2.], [2., 0., 0.], [0., 1., -1.]])
X_train_result = preprocessing.scale(X_train, axis=0) #axis=0表示按列进行标准化
print(X_train_result)
print(X_train_result.mean(axis=0)) #均值为0
print(X_train_result.std(axis=0))  #标准差为1

输出结果如下：

[[ 0.         -1.22474487  1.33630621]
 [ 1.22474487  0.         -0.26726124]
 [-1.22474487  1.22474487 -1.06904497]]
[0. 0. 0.]
[1. 1. 1.]

如果在做机器学习模型训练的时候，想把训练集的缩放标准应用到测试集上，那就要使用StandardScaler()这个类了。代码如下：

from sklearn import preprocessing
import numpy as np

X_train = np.array([[1., -1., 2.], [2., 0., 0.], [0., 1., -1.]])
scaler = preprocessing.StandardScaler().fit(X_train)
X_scaled = scaler.transform(X_train)
print(X_scaled.mean(axis=0)) #均值为0
print(X_scaled.std(axis=0))  #标准差为1
X_test = [[-1., 1., 0.]]     #使用训练集的缩放标准来标准化测试集，这里的缩放标准指的就是训练集的列的均值和标准差
print(scaler.transform(X_test))

输出结果如下：

[0. 0. 0.]
[1. 1. 1.]
[[-2.44948974  1.22474487 -0.26726124]]

二.归一化

归一化就是把数据压缩到一个区间内，比如[0,1]、[-1,1]。常用的2种方法如下：

1.Min-Max Normalization

用方程表示如下：

归一化的区间范围是[0,1]。代码实现如下：

import numpy as np
from sklearn import preprocessing as pp
X_train = np.array([[ 1., -5., 8.], [ 2., -3., 0.], [ 0., -1., 1.]])
scaler = pp.MinMaxScaler().fit(X_train) #默认数据压缩范围为[0,1]
print(scaler.transform(X_train))

输出结果如下：

[[0.5   0.    1.   ]
 [1.    0.5   0.   ]
 [0.    1.    0.125]]

2.Mean Normalization

用方程表示如下：

归一化的区间范围是[-1,1]。

import numpy as np
from sklearn import preprocessing as pp
X_train = np.array([[ 1., -5., 8.], [ 2., -3., 0.], [ 0., -1., 1.]])
scaler = pp.MinMaxScaler(feature_range=(-1, 1)) #设置数据压缩范围为[-1,1]
scaler = scaler.fit(X_train)
print(scaler.transform(X_train))

输出结果如下：

[[ 0.   -1.    1.  ]
 [ 1.    0.   -1.  ]
 [-1.    1.   -0.75]]

上述代码主要使用scikit-learn的预处理子模块preprocessing提供MinMaxScaler类来实现归一化功能。MinMaxScaler类有一个重要参数feature_range，该参数用于设置数据压缩的范围，默认值是[0,1]。

三.正则化

  简单理解使用正则化的目的就是为了防止过拟合，当然还有其它防止过拟合的方法，比如降低特征维度。先举个例子说下为什么降低特征维度也可以防止过拟合，然后再说明正则化是如何防止过拟合的。首先要搞明白过拟合的本质是什么？就是把噪音也当做事物的特征进行了建模。假如一只小鸟受伤了，暂时不会飞翔，在构建鸟类分类器的时候，把能否飞翔这个噪音也学习成模型的特征了，这样正常的能够飞翔的小鸟就判断为不是鸟类了，当然这是一个过拟合的很牵强的例子，但是也可说明一定的问题。正则化是如何防止过拟合的呢？
对于给定的数据集$D=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_m,y_m\right)\right\}$，考虑最简单的线性回归模型，以平方误差作为损失函数，优化目标如下：

引入L2范数正则化，称为岭回归[ridge regression]，如下所示：

引入L1范数正则化，称为LASSO[Least Absolute Shrinkage and Selection Operator]回归，如下所示：

假设数据维度为2维，通过方程$\sum _{j=1}^M{\left|{}_j\right|}^q\le \frac{1}{\lambda }$(这里没有展开推导，若感兴趣可参考[3])可以做出下图，其中左图即$w_1^2+w_2^2\le \frac{1}{\lambda }$，右图即$\left|w_1\right|+\left|w_2\right|\le \frac{1}{\lambda }$。可见随着$\lambda$增大，越来越多的参数会变为0：

  目的是为了找到损失函数取最小值时对应的权重值，其中下图蓝色圆圈是平方误差项等值线，当取椭圆中心点时，损失函数(这里说的损失函数不包含正则化)值最小。总的损失函数(这里说的损失函数包含正则化)就是求蓝圈+红圈的和的最小值。
  正则化方法是一个常量，它通过限制模型的复杂度，使得复杂的模型能够在有限大小的数据集上进行训练，而不会产生严重的过拟合。正则项越小，惩罚力度越小，极端情况正则项为0时，就会造成过拟合问题；正则化越大，惩罚力度越大，就会容易出现欠拟合问题。

  通过上图可以直观的看到采用L1范数时平方误差项等值线与正则化项等值线的交点出现在坐标轴上，即$w_1=0$或者$w_2=0$。当采用L2范数时，两者的交叉点常出现在某个象限中，即$w_1\ne 0$且$w_2\ne 0$。这样采用L1正则化比L2正则化更容易得到稀疏解。L2正则化优势是处处可导，L1正则化有拐点，不是处处可微，但可以得到更加稀疏的解。