轻松搞懂Python递归函数的原理与应用

1、递归的原理

学习任何计算机语言过程中，“递归”一直是所有人心中的疼。不知你是否听过这个冷笑话：“一个面包，走着走着饿了，于是就把自己吃了”。

呵呵。

常理推断，特别是解释型语言，当程序执行函数内部的语句时，这个函数还没有定义完，没定义完怎么可以调用本身呢。

但实质上，当你执行函数内部的语句时，一定有函数外部的语句调用了这个函数，此时该函数的所有代码和语句，已经在内存中形成了逻辑，这就是递归函数的原理。

在Python当中很重要的就是递归的使用。

2、递归的玩法

牛叔语录：人类创造出的任何复杂的概念，都是为了让事情变得更简单一些。

递归是为了更好的解决，“自已定义自己”的数学或是哲学难题。

用好递归，有2个、2个、2个（重要的事情说3遍）要点，必须要同时注意，下面请各位评委看我的表演。

(1) 认清自己

认清自己是递归玩法的核心。与处理任何事情一样，首先要问的就是：如何准确地定义好“当前要做的事情”。处理好这个问题，我们就已经成功了一半。

此处我们拿数学函数为例， 因为数学函数的定义有公式，显而易见，它的意义就是根据变量来计算出结果，最容易被小白理解，栗子如下：

假设数学函数：

f(n) = (f(n-1) + 1)*2 ，告诉你f(1)=1，问f(10)是多少？

我们直接把这个f(n)定义成函数，并且计算f(10) 如下：

def f(n):
    if n==1:
        return 1
    else:
        return (f(n-1)+1)*2

print(f(10))

结果是1534，运行正确。恭喜你这是一道著名的数学难题，你竟然轻松解决了，原题这样：

猴子有一堆桃子，每天吃前一天剩下的一半多1个，昨天吃完发现剩了1个，那么前10天它剩下多少个桃子？

我们公式中的n就表示前n天，公式结果就表示剩下了多少桃子，昨天的桃子y总比今天的x有这样的关系：x = y/2 -1 所以：y=(x+1)*2，这个就是上面的公式。

在写本递归函数时，语句基本上照抄数学公式，我们不知道解题过程就能求出答案，真是太神奇了！只要定义好，递归跑不了！慢着，别下结论，我们再看看如下的点。

（2）把握好方向

与上面的“猴子摘桃”同一个问题，原题我们改一下说法，问：

猴子第1天摘了一堆桃子吃了一半又多一个，第2天吃了剩下的一半又多一个，...，第10天早上时发现只有1个桃子了。问第1天摘了多少？这回我们把n设为第n天（而不是前n天）

与上面函数f类似，后项也是根据前项值来确定，为区别我们使用g()代表该函数:

g(n) = g(n-1)/2 -1 ，告诉你 g(10)=1，问g(1) 是多少？

牛叔说了，“只要定义好，递归跑不了”，我们先不管三七二十一，照抄上面的数学公式，“迅速而又准确”地把g(n)函数用如下的代码造了出来，如下：

def g(n):
    if n==10:
        return 1
    else:
        return g(n-1)/2 - 1

print(g(1))

 运行后却出现了如下的错误，提示递归溢出！

 这是怎么回事呢？因为我们还有第2个点，您没有注意！

这个点就是 “要想递归不出错，开车方向不能错”，这个方向是指: 程序求解的方向必须和定义的方向相同，

此处我们要根据n=10的结果来求n=1，方向是：后项(10)->前项(1)，而程序中翻译的公式是 前项（n-1)->后项(n)，根据公式写的程序，也只能完成公式的求解顺序，即：n从小到大的推导，

所以此时如果求g(100)，结果是这样的，完全没有问题（但没有任何意义）：

所以此处要通过我们的智慧把这个公式，“颠倒”过来变成：

g(n-1) = (g(n)+1) * 2    => g(n) = (g(n+1)+1) * 2 

这样根据公式写的代码，就可以完成从后项（n+1)推导到前项（n)的功能了！ 

如果不理解，小学二年级的代数再看一遍，具体程序如下：

1 def g(n):
2     if n==10:
3         return 1
4     else:
5         return 2*(g(n+1)+1)
6 
7 print(g(1))

终于得出了正确的结果，1534。答案和第1题一样！猴子终于满意了，10天的口粮有着落了。 

3、分解质因数练习

小学生专用名词，别给吓住了，其实就是把数字分解成不能再分解的乘法，比如：8=2*2*2， 10 = 2*5，而不是 8 = 2 * 4 这种可以再分解的。

此递归问题，是编程竞赛常客，拿来练手比较合适。如下Python代码，对于本问题的解答充分说明了递归的方便之处，以分解了980这个整数为示例：

1 def defactor(N):  #定义一个函数名称为defactor，意义是返回N的所有因子
2     for i in range(2,N): #从2开始试试
3         if N%i ==0: #如果试到i是N的因子的话，就返回i的所有因子和N/i的所有因子 的列表
4             return defactor(i)+defactor(int(N/i))
5     else:#如果没有试到就说明这个N是一个质数，就直接包含它的 列表
6         return [N]
7         
8 print(defactor(980))

运行的答案是：

[2, 2, 5, 7, 7]

Bingo，在这里函数defactor(N) 

（1）定义:  求出参数N所有因子的数组，

（2）方向：整数 -> 最小的质数

首先，理解else:部分（代码中的第5，6两行），

这是函数的，把方向的部分，小牛叔称他为：结果产生部分，它能确保程序不会跑偏的代码，如果传入的数字N没有可以被整除的数字，即循环到头了，才会执行这个部分，每一个质数因子都会从这个部分产生，因为最终的结果只能是质数。下图树中的所有叶节点（没有子节点的叶子：2，2，5，7，7），就是从这个部分产生的，当执行到这个部分时，程序不会再往向下递归，所以不会产生下层的树型结构。

再理解，递归的部分（2，3，4行）

通过循环来试因子，如果试到i是N的因子（即N可以被i整除）的话，就返回i的所有因子和 N/i的所有因子 组成的列表，因此下图中所有从上到下的两个箭头对，就代表着这两个递归调用。

通过这个树形解题的过程，您会更加明白！

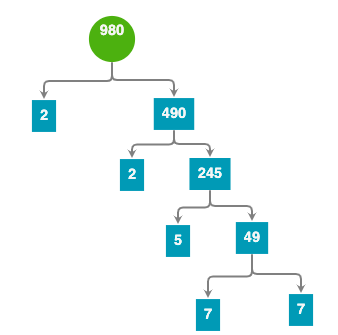
在整个程序递归执行时，看起来是从顶980开始向下求解执行，而求解的过程中结果却是从最下层的7，7开始向上汇集。