DL之DNN优化技术:神经网络算法简介之GD/SGD算法的简介、代码实现、代码调参之详细攻略
DL之DNN优化技术:神经网络算法简介之GD/SGD算法的简介、代码实现、代码调参之详细攻略
目录
GD算法的简介
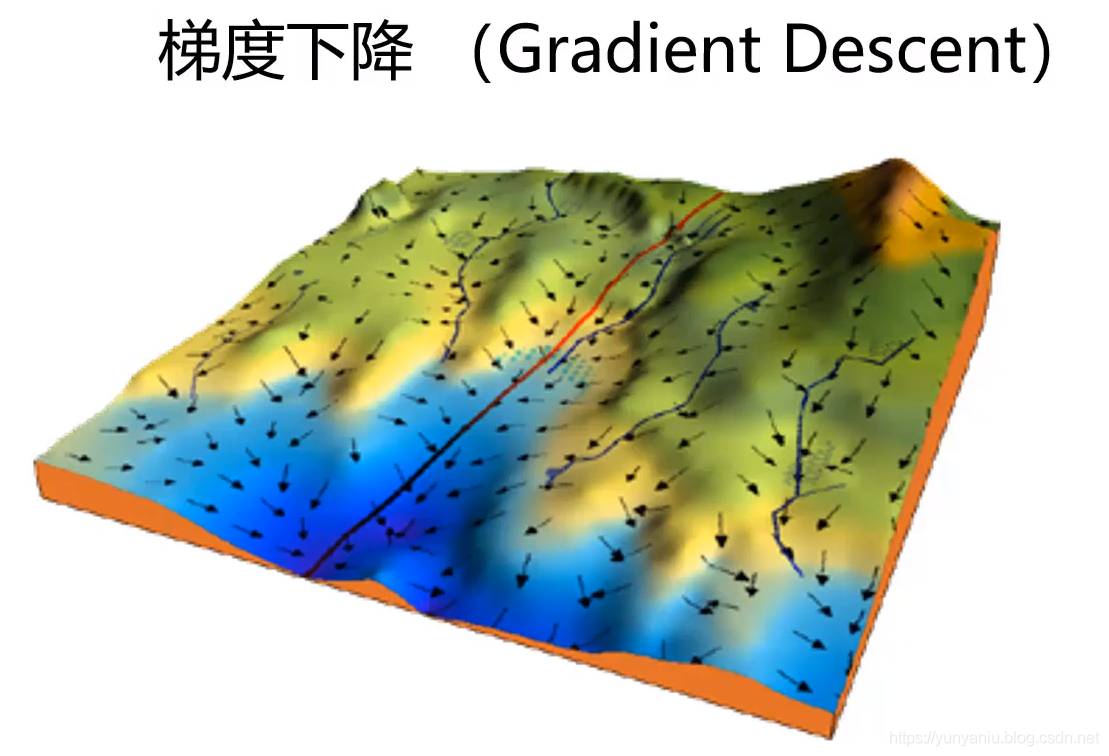
GD算法,是求解非线性无约束优化问题的基本方法,最小化损失函数的一种常用的一阶优化方法。如图所示,找出最陡峭的方向作为下山的方向。
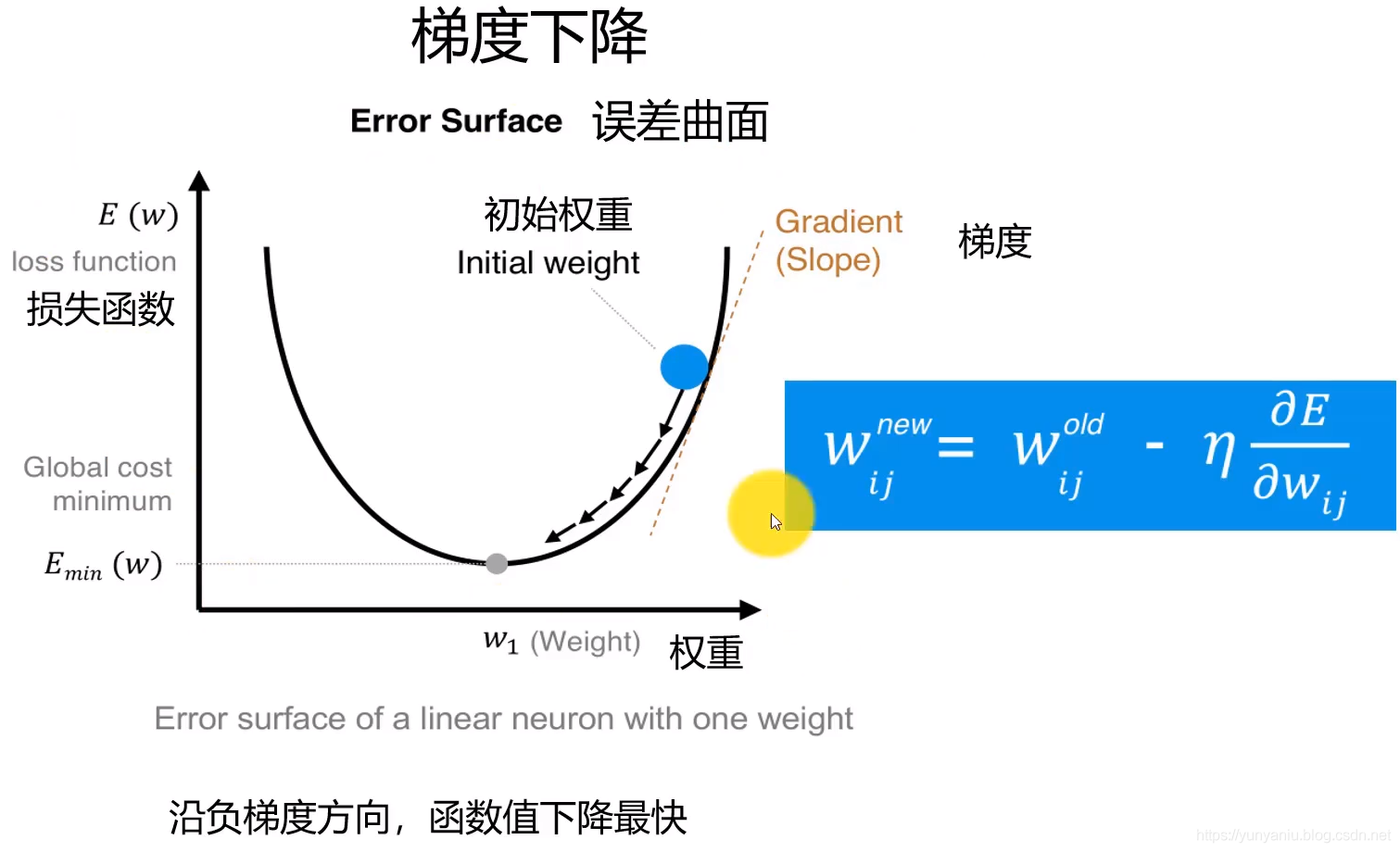
1、如何求梯度?
沿着梯度方向,函数值下降最快。
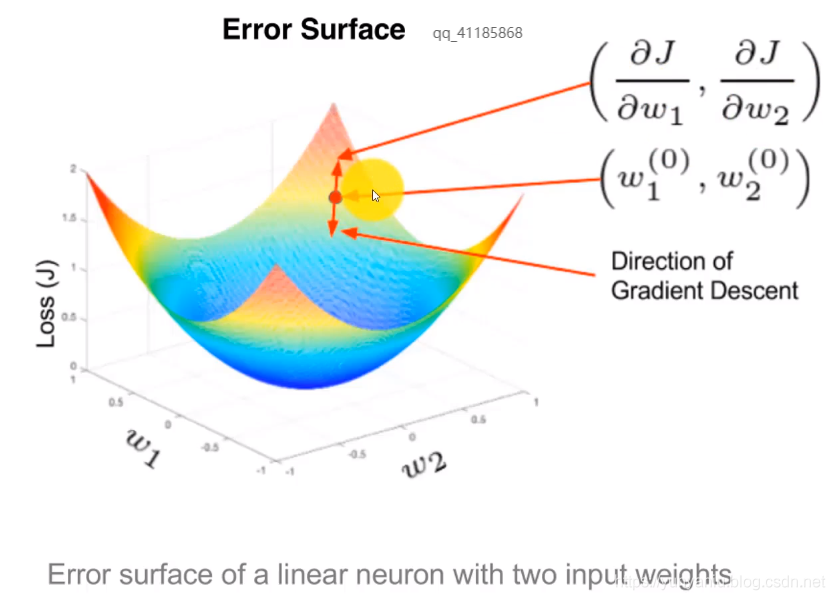
2、二元曲面
具有两个输入权重的线性神经元的误差曲面,Error surface of a linear neuron with two input weights
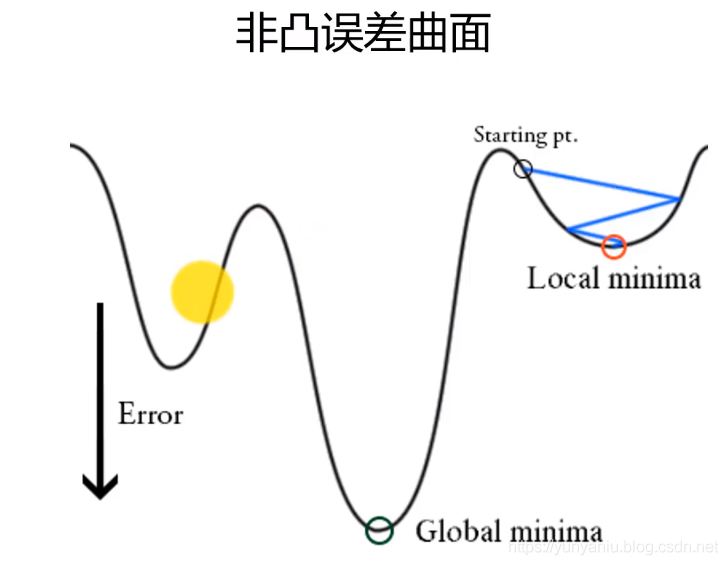
3、GD算法容易陷入局部最小值
GD/SGD算法的代码实现
1、Matlab编程实现
- %% 最速下降法图示
- % 设置步长为0.1,f_change为改变前后的y值变化,仅设置了一个退出条件。
- syms x;f=x^2;
- step=0.1;x=2;k=0; %设置步长,初始值,迭代记录数
- f_change=x^2; %初始化差值
- f_current=x^2; %计算当前函数值
- ezplot(@(x,f)f-x.^2) %画出函数图像
- axis([-2,2,-0.2,3]) %固定坐标轴
- hold on
- while f_change>0.000000001 %设置条件,两次计算的值之差小于某个数,跳出循环
- x=x-step*2*x; %-2*x为梯度反方向,step为步长,!最速下降法!
- f_change = f_current - x^2; %计算两次函数值之差
- f_current = x^2 ; %重新计算当前的函数值
- plot(x,f_current,'ro','markersize',7) %标记当前的位置
- drawnow;pause(0.2);
- k=k+1;
- end
- hold off
- fprintf('在迭代%d次后找到函数最小值为%e,对应的x值为%e\n',k,x^2,x)
2、基于python实现SGD算法
- class SGD:
- def __init__(self, lr=0.01):
- self.lr = lr 学习率,实例变量
-
- update()方法,在SGD中会被反复调用
- def update(self, params, grads):
- for key in params.keys():
- params[key] -= self.lr * grads[key] 参数params、grads依旧是字典型变量,按params['W1']、grads['W1']的形式,分别保存了权重参数和它们的梯度。
-
- '伪代码:神经网络的参数的更新'
- network = TwoLayerNet(...)
- optimizer = SGD()
- for i in range(10000):
- ...
- x_batch, t_batch = get_mini_batch(...) mini-batch
- grads = network.gradient(x_batch, t_batch)
- params = network.params
- optimiz
GD算法的改进算法
1、SGD算法
(1)、mini-batch
如果不是每拿到一个样本即更改梯度,而是若干个样本的平均梯度作为更新方向,则是mini-batch梯度下降算法。
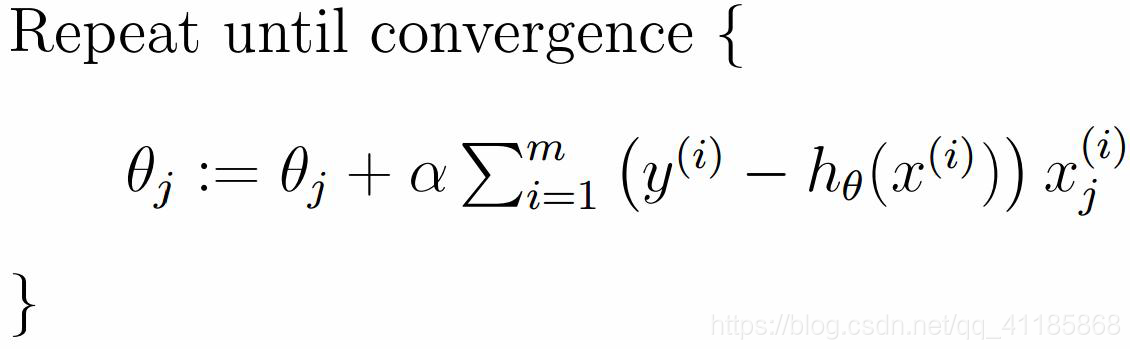
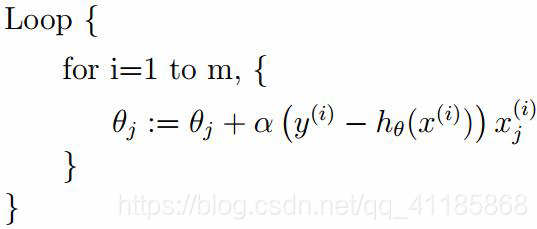
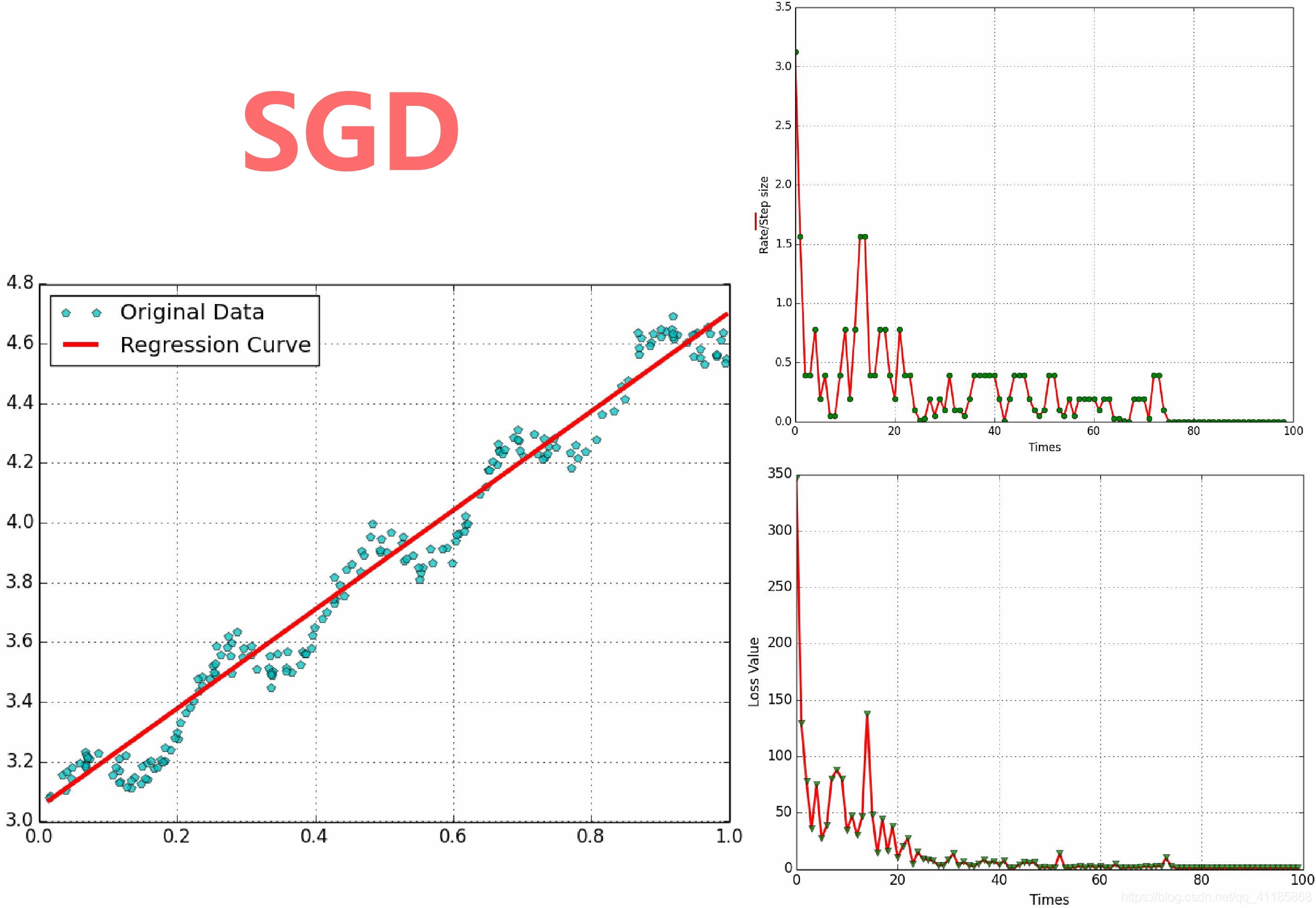
(1)、SGD与学习率、Rate、Loss
GD算法中的超参数
1、学习率
(1)、固定学习率实验的C代码

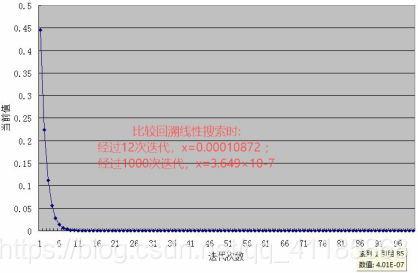
(2)、回溯线性搜索(Backing Line Search)
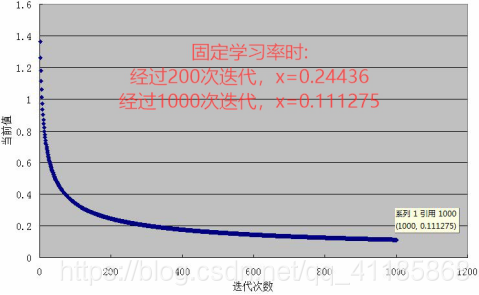
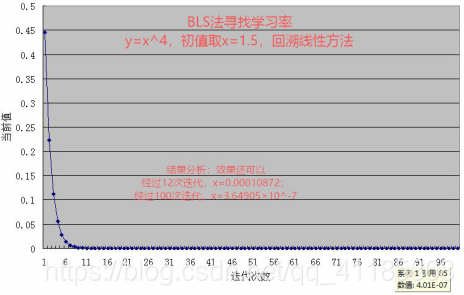
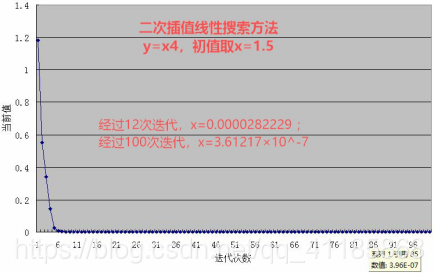
(3)、二次插值线性搜索:回溯线性搜索的思考——插值法,二次插值法求极值

网站声明:如果转载,请联系本站管理员。否则一切后果自行承担。
赞同 0
评论 0 条
- 上周热门
- 银河麒麟添加网络打印机时,出现“client-error-not-possible”错误提示 1323
- 银河麒麟打印带有图像的文档时出错 1236
- 银河麒麟添加打印机时,出现“server-error-internal-error” 1023
- 统信桌面专业版【如何查询系统安装时间】 951
- 统信操作系统各版本介绍 944
- 统信桌面专业版【全盘安装UOS系统】介绍 903
- 麒麟系统也能完整体验微信啦! 889
- 统信【启动盘制作工具】使用介绍 499
- 统信桌面专业版【一个U盘做多个系统启动盘】的方法 440
- 信刻全自动档案蓝光光盘检测一体机 386
- 本周热议
- 我的信创开放社区兼职赚钱历程 40
- 今天你签到了吗? 27
- 信创开放社区邀请他人注册的具体步骤如下 15
- 如何玩转信创开放社区—从小白进阶到专家 15
- 方德桌面操作系统 14
- 我有15积分有什么用? 13
- 用抖音玩法闯信创开放社区——用平台宣传企业产品服务 13
- 如何让你先人一步获得悬赏问题信息?(创作者必看) 12
- 2024中国信创产业发展大会暨中国信息科技创新与应用博览会 9
- 中央国家机关政府采购中心:应当将CPU、操作系统符合安全可靠测评要求纳入采购需求 8
热门标签更多


